【電験三種_理論】2021年(令和３年) 問１８の過去問解説

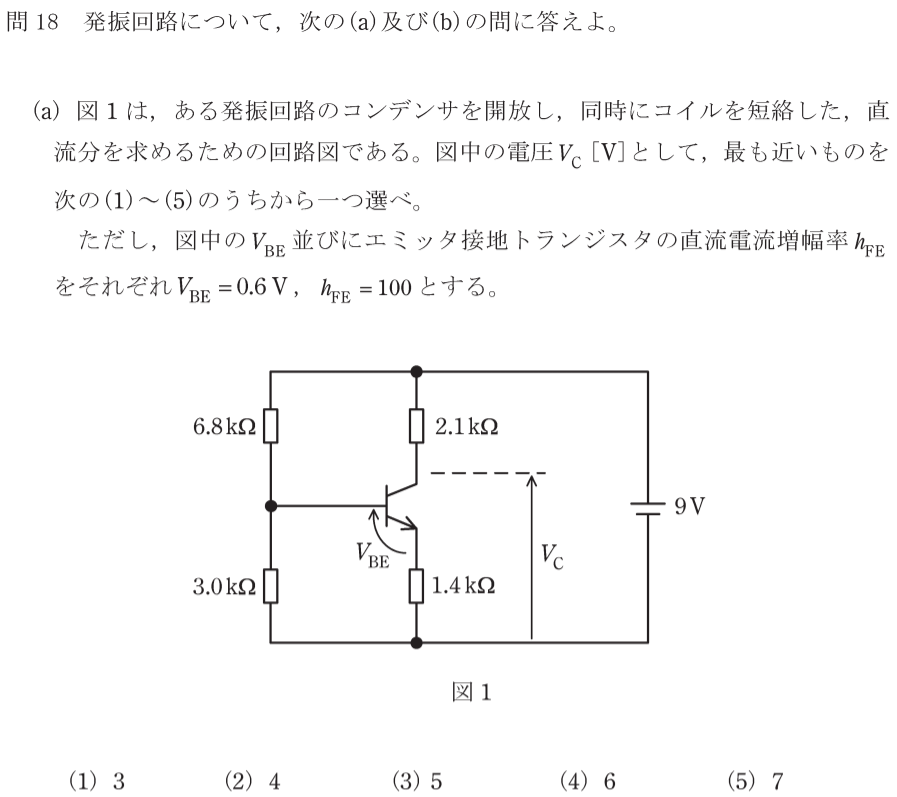
(a) 【電験三種理論2021年令和３年問１８】

ポイント

ベース電流は小さいため、ベース電位$V_{B}$は、6.8kΩと3.0kΩの分圧により求める。

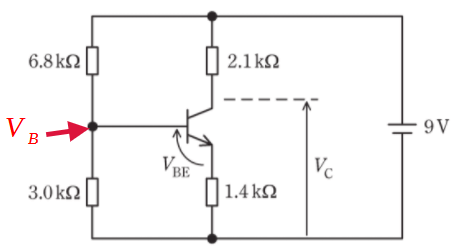
直流電流増幅率$h_{FE}$が大きく、コレクタ電流に比べてベース電流が十分小さいため、コレクタ電流＝エミッタ電流とみなせる。

解説

ベース電位は分圧で計算すると以下の通り。

$$V_{B}=9×\frac{3}{6.8+3}=2.76 \mathrm{ [V]} $$

エミッタ電位$V_{E}=V_{B}-V_{BE}$より、$V_{E}=2.76-0.6＝2.16 \mathrm{ [V]} $とわかる。

よって、エミッタ電流は、

$$I_{E}=\frac{2.16}{1.4×10^3} \mathrm{ [A]} $$

コレクタ電流は、上述のポイントで示した通りエミッタ電流と等しいとみなせるので（$I_{C}\approx I_{E}$）、

$$V_{C}=9-I_{E}×2.1×10^3=5.76 \ \mathrm{ [V]} $$

よって、最も値が近い選択肢は（４）である。

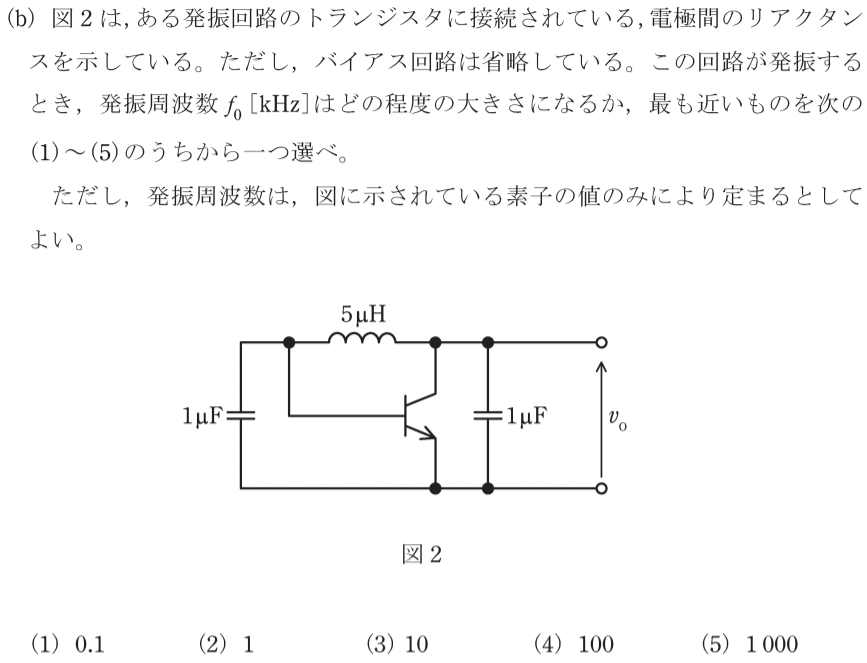
(b) 【電験三種理論2021年令和３年問１８】

ポイント

この発振回路は、コンデンサ二つとコイル一つから成るので、コルピッツ発振回路である。

コルピッツ発振回路の発振条件は、直列共振条件と同じであり、二つのコンデンサの直列合成静電容量を$C$とおくと、以下となる。

$$2\pi f L=\frac{1}{2\pi f C} \Leftrightarrow f=\frac{1}{2\pi \sqrt{LC}}$$

解説

二つのコンデンサの直列分の合成静電容量は0.5[μF]なので、発振周波数は以下の通り。

$$f_{0}=\frac{1}{2\pi \sqrt{5×0.5×10^{-12}}}\approx 100 \ \mathrm{ [kHz]} $$

よって、正解は（４）である。