- 旧帝大 修士卒(電気電子工学専攻)
- 電験一種に、10ヶ月で合格
- 気象予報士試験に、4ヶ月で合格
- 電験三種や電工の動画による問題解説サービスを実施中
- YouTubeチャンネル「電験大学」は登録者数3000人以上
- 電気工事士試験の受験生向けYouTubeチャンネルも開設

解説
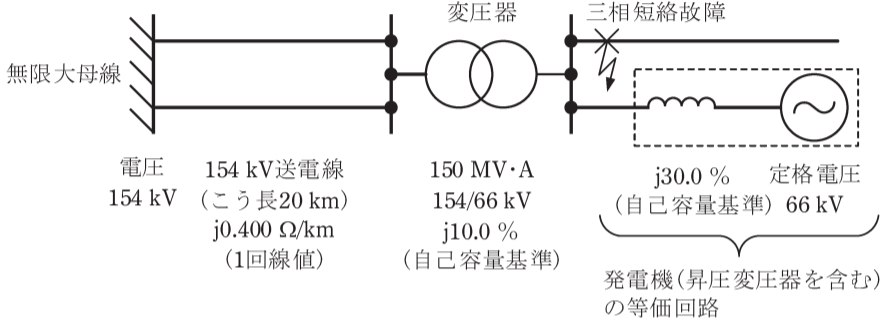
単位法を用いた系統の故障電流計算の問題です。
(1)基準電流と基準インピーダンスを求めよ

※補助単位(kとM)の取り扱いに注意して計算しましょう!
a)基準電流を求めよ
(基準容量)=$\sqrt{3}$(基準電圧)×(基準電流)より、
$$\begin{eqnarray} I_{B} \ \mathrm{[kA]}&=& \frac{100 \ \mathrm{[MVA]}}{\sqrt{3}×154 \ \mathrm{[kV]}} \\ &≒& 0.3749 \\ &≒& 0.375 \ \mathrm{[kA]} \end{eqnarray}$$
b)基準インピーダンスを求めよ
(基準電圧)=$\sqrt{3}$ (基準電流)×(基準インピーダンス)より、
$$\begin{eqnarray} Z_{B} \ \mathrm{[Ω]}&=& \frac{154 \ \mathrm{[kV]}}{ \sqrt{3} × 0.3749 \ \mathrm{[kA]}} \\ &≒& 237.2 \\ &≒& 237 \ \mathrm{[Ω]} \end{eqnarray}$$
(2)インピーダンスや電流値を単位法で表せ

a)線路インピーダンス
題意のインピーダンス[Ω]は、$\mathrm{j}0.400 \ \mathrm{[Ω/km]}×20 \ \mathrm{[km]}= \mathrm{j} 8.00 \ \mathrm{[Ω]}$である。
(1)b)より、基準電圧154 kV、基準容量100 MVAの場合の基準インピーダンスは237.2 Ωなので、
これらの比率から単位法の値[p.u.]を計算すると次のようになる。
$$\begin{eqnarray} \frac{ \mathrm{j} 8.00}{237.2} &≒& \mathrm{j} 0.03373 \\ &≒& \mathrm{j} 0.0337 \ \mathrm{[p.u.]} \end{eqnarray}$$
b)変圧器インピーダンス
変圧器インピーダンスj10.0%を自己容量ベース(150MVA)から100MVAベースへ変換すると、
$$\begin{eqnarray} \mathrm{j}10.0×\frac{100}{150}&≒&\mathrm{j} 6.667 \ \mathrm{[\%]} \\ &=& \mathrm{j} 0.06667 \ \mathrm{[p.u.]} \mathrm{(∵100\%=1p.u.)} \\ &≒& \mathrm{j} 0.0667 \ \mathrm{[p.u.]} \end{eqnarray}$$
となる。
c)変圧器二次電流
基準電圧66kV、基準容量100MVAの場合の基準電流[kA]は、$\dfrac{100 \ \mathrm{[MVA]}}{\sqrt{3}×66 \ \mathrm{[kV]}}≒0.8748 \ \mathrm{[kA]}$となる。
よって25kAを単位法で表すと、
$$\begin{eqnarray} \frac{25 \ \mathrm{[kA]}}{0.8748 \ \mathrm{[kA]} }&≒&28.58 \ \mathrm{[p.u.]} \\ &≒& 28.6 \ \mathrm{[p.u.]} \end{eqnarray}$$
となる。
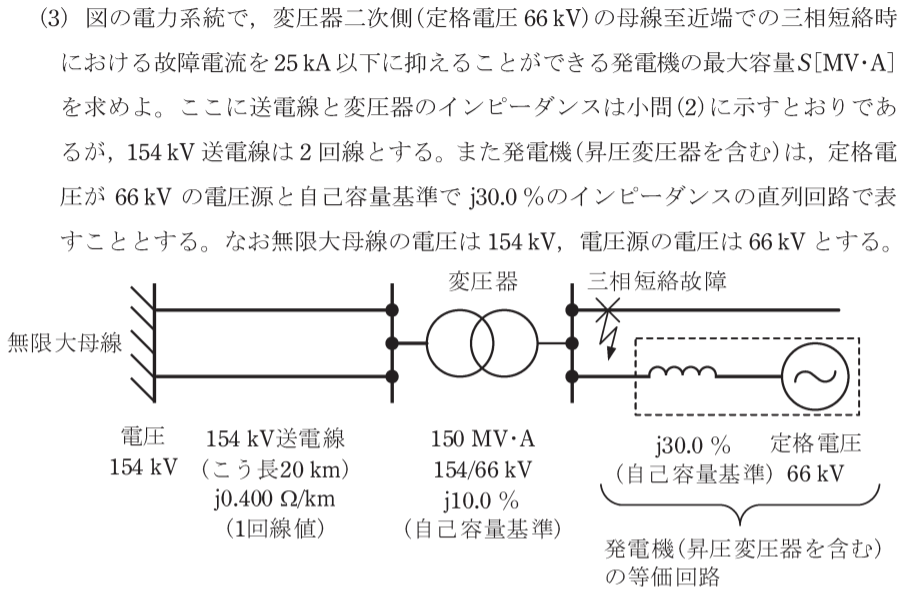
(3)故障電流計算
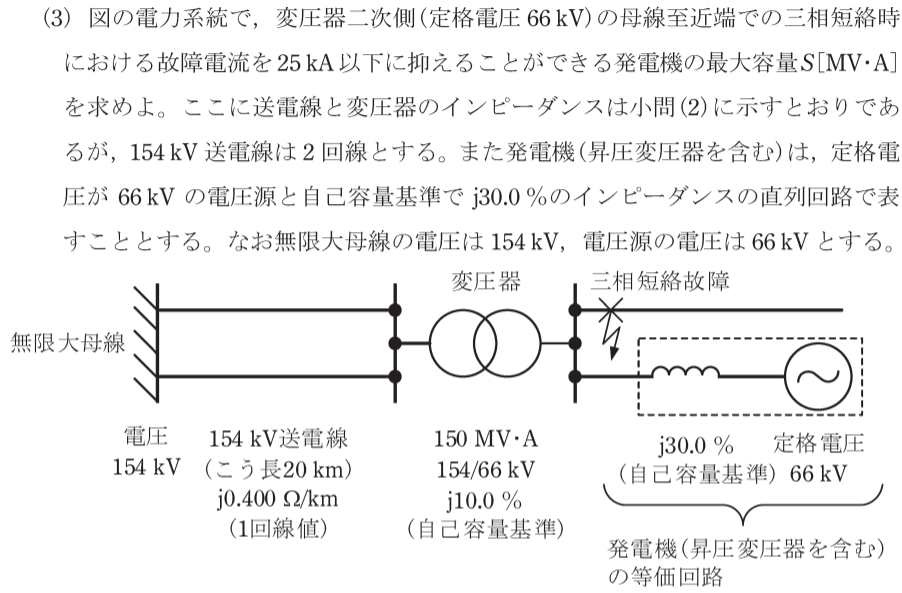
二回線の送電線のインピーダンスは、一回線分のインピーダンスの半分となるので、 j0.01687 [p.u.]となる。
発電機インピーダンスは100MVAベースに変換し、単位法で表すと、
$$ \frac{\mathrm{j}30.0 \ \mathrm{\%}}{100}×\frac{100 \ \mathrm{[MVA]}}{S \ \mathrm{[MVA]}} = \frac{\mathrm{j}30.0 }{S} \ \mathrm{[p.u.]}$$
故障点から見た電源側インピーダンス$Z$は、次の二つのインピーダンスの並列となる。
- 上位系(変圧器+154kV送電線)を見たインピーダンス
- 発電機を見たインピーダンス
よって、故障点から見た電源側インピーダンス$Z$は、 並列の合成インピーダンスの公式から、
$$\begin{eqnarray} Z&=& \frac{1}{\frac{1}{\mathrm{j}0.01687 + \mathrm{j}0.06667} + \frac{1}{ \frac{\mathrm{j}30.0 }{S} }} \\ &=& \frac{( \mathrm{j}0.01687 + \mathrm{j}0.06667 )× \frac{\mathrm{j}30.0 }{S} }{( \mathrm{j}0.01687 + \mathrm{j}0.06667 )+ \frac{\mathrm{j}30.0 }{S} } \\ &=& \frac{ \mathrm{j}2.506}{ 0.08354S + 30} \ \mathrm{[p.u.]}\end{eqnarray}$$
これにより、三相短絡電流[p.u.]は次のように求まる。
$$\frac{1}{Z}=\frac{ 0.08354S + 30 }{ \mathrm{j}2.506 } \ \mathrm{[p.u.]}$$
三相短絡電流を25kA((2)c)より28.58[p.u.])以下にできる発電機の最大容量は、
$$\begin{eqnarray} |\frac{ 0.08354S + 30 }{ \mathrm{j}2.506 }| &≦&28.58 \ \mathrm{[p.u.]} \\ ⇔ S &≦&498.22… \\ &≒& 498 \ \mathrm{[MVA]} \end{eqnarray}$$

