- 旧帝大 修士卒(電気電子工学専攻)
- 電験一種に、10ヶ月で合格
- 気象予報士試験に、4ヶ月で合格
- 電験三種や電工の動画による問題解説サービスを実施中
- YouTubeチャンネル「電験大学」は登録者数3000人以上
- 電気工事士試験の受験生向けYouTubeチャンネルも開設

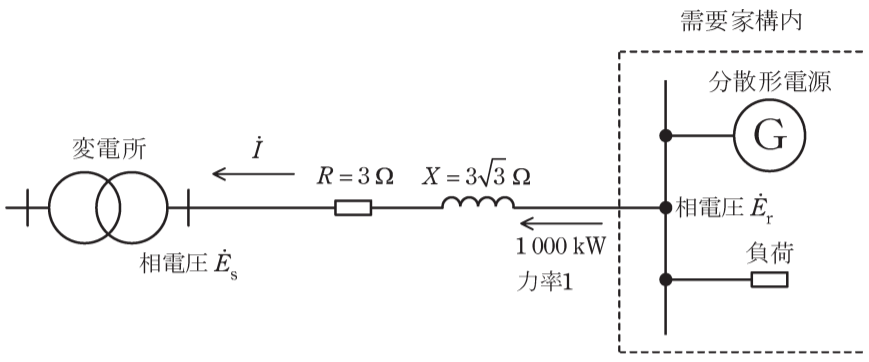
解説
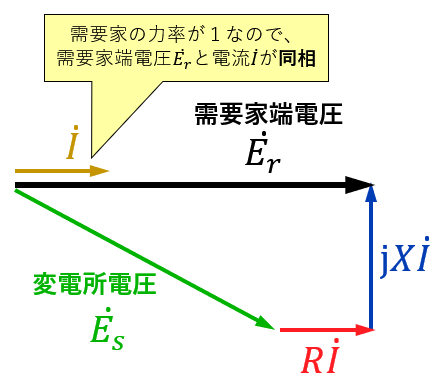
(1)変電所ー需要家端のベクトル図

力率1で逆潮流しているため、変電所電圧<需要家電圧となっていることを意識して解答するとよい。
関係式とベクトル図は以下の通りです。
力率が1ということで、電流ベクトルがどちらの電圧ベクトルと同じ向き(同相)なのかがポイントです。
$$\dot{E_r}=\dot{E_s}+R\dot{I}+\mathrm{j}X\dot{I}$$
(2)需要家端電圧を求めよ

$P=\sqrt{3}VIcos{θ}$より、線電流$I$は
$$\begin{eqnarray}I&=&\frac{P}{ \sqrt{3}V\cos{θ} } \\ &=& \frac{1000×10^3 \ \mathrm{W}}{ \sqrt{3}(\sqrt{3}E_r)×1} \\ &=& \frac{1000×10^3}{ 3E_r} \ \mathrm{[A]} \end{eqnarray}$$
ベクトル図から、下記の黄色の直角三角形にて三平方の定理より、
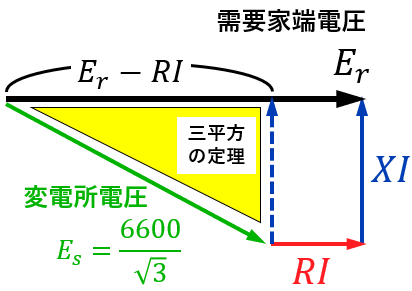
$$\begin{eqnarray} E_s^2 &=& (E_r-RI)^2+(XI)^2 \\ ⇔ \left(\frac{6600}{\sqrt{3}}\right)^2 &=& \left(E_r -3 \frac{1000×10^3}{ 3E_r} \right)^2 +\left(3\sqrt{3} \frac{1000×10^3}{ 3E_r} \right)^2 \\⇔E_r^2 &=& 16.27×10^6 , 0.246×10^6(\mathrm{後者は不適}) \\ ∴ E_r &=& 4.034×10^3 \ \mathrm{[V]} \end{eqnarray}$$
これは相電圧であるので、線間電圧を求めるためには$\sqrt{3}E_r$を計算する必要がある。
$$ \begin{eqnarray} \sqrt{3}E_r &=& \sqrt{3} ×4.034×10^3 \\ &≒&6990 \ \mathrm{[V]} \end{eqnarray} $$
三平方の定理以降の展開において、解の公式などを使用する中で計算ミスをしやすいので、余裕があれば検算しましょう。
検算する際には以下の三平方の定理の式に$E_r$を代入してみるとよいと思います。
$$ \left(\frac{6600}{\sqrt{3}}\right)^2 = \left(E_r -3 \frac{1000×10^3}{ 3E_r} \right)^2 +\left(3\sqrt{3} \frac{1000×10^3}{ 3E_r} \right)^2 $$
上記ができなくても、最低限、変電所電圧より需要家端電圧が高くなっていることは確認しておきましょう!

